Authors:
(1) J. Quetzalcóatl Toledo-Marín, University of British Columbia, BC Children’s Hospital Research Institute Vancouver BC, Canada (Email: j.toledo.mx@gmail.com);
(2) James A. Glazier, Biocomplexity Institute and Department of Intelligent Systems Engineering, Indiana University, Bloomington, IN 47408, USA (Email: jaglazier@gmail.com);
(3) Geoffrey Fox, University of Virginia, Computer Science and Biocomplexity Institute, 994 Research Park Blvd, Charlottesville, Virginia, 22911, USA (Email: gcfexchange@gmail.com).
Table of Links
5 Conclusions
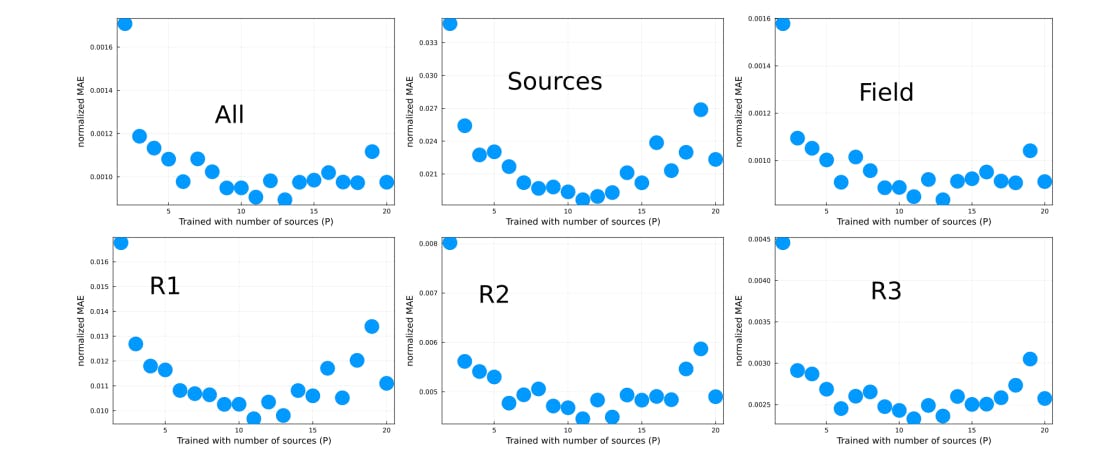
When selecting a NN for a specific task, it is important to consider the function and requirements of the task at hand. There is currently no consensus on which NN is optimal for a given task, primarily due to the large number of NN options available, the rapidly evolving nature of the field, and the lack of a comprehensive deep learning theory. This leads to a reliance on empirical results. Our paper is an important step at establishing best practices for this type of problems. we focused on randomly placed sources with random fluxes which yield large variations in the field. Our method can be generalized for different diffusion equations.
As part of future steps, we will increase the complexity of the problem being solved by considering conditions closer to real-problems, i.e., by considering less symmetrical sources, different diffusivities and different boundary conditions. In addition, further design is required for these models to be used in a production environment in a reliable way, i.e., how to deal with error performance edge cases on-the-fly? Ultimately, to be able to deploy the model for production, one requires a method to keep the performance error below a predefined bound. For instance, one can train an additional NN that takes the predicted stationary solution and predicts the initial condition, which is then compared with the ground truth initial condition. This framework allows a comparison between ground truth input and predicted input without requiring the ground truth steady-state solution. However, this approach would only be reliable if the input error is always proportional to the steady-state error and hence requires further investigation. A perhaps simpler approach consists in sampling the NN’s output for the same input using a drop-out feature, such that if the fluctuations from the samples are small enough, then the NN’s prediction is robust enough. Both cases require benchmark design. We have developed a process in this paper that can easily be replicated for more complicated problems of this type, and provided a variety of benchmarks.
6 Acknowledgements
JQTM acknowledges a Mitacs Postdoctoral Fellowship. GCF acknowledges partial support from DOE DE-SC0023452 and NSF OAC-2204115.
References
[1] William E Schiesser. The numerical method of lines: integration of partial differential equations. Elsevier, 2012.
[2] Amir Barati Farimani, Joseph Gomes, and Vijay S Pande. Deep learning the physics of transport phenomena. arXiv preprint arXiv:1709.02432, 2017.
[3] Rishi Sharma, Amir Barati Farimani, Joe Gomes, Peter Eastman, and Vijay Pande. Weakly-supervised deep learning of heat transport via physics informed loss. arXiv preprint arXiv:1807.11374, 2018.
[4] Haiyang He and Jay Pathak. An unsupervised learning approach to solving heat equations on chip based on auto encoder and image gradient. arXiv preprint arXiv:2007.09684, 2020.
[5] Mohammad Edalatifar, Mohammad Bagher Tavakoli, Mohammad Ghalambaz, and Farbod Setoudeh. Using deep learning to learn physics of conduction heat transfer. Journal of Thermal Analysis and Calorimetry, pages 1–18, 2020.
[6] Angran Li, Ruijia Chen, Amir Barati Farimani, and Yongjie Jessica Zhang. Reaction diffusion system prediction based on convolutional neural network. Scientific reports, 10(1):1–9, 2020.
[7] Zongyi Li, Nikola Kovachki, Kamyar Azizzadenesheli, Burigede Liu, Kaushik Bhattacharya, Andrew Stuart, and Anima Anandkumar. Fourier neural operator for parametric partial differential equations. arXiv preprint arXiv:2010.08895, 2020.
[8] Shengze Cai, Zhicheng Wang, Sifan Wang, Paris Perdikaris, and George Karniadakis. Physics-informed neural networks (pinns) for heat transfer problems. Journal of Heat Transfer, 2021.
[9] Geoffrey Fox and Shantenu Jha. Learning everywhere: A taxonomy for the integration of machine learning and simulations. In 2019 15th International Conference on eScience (eScience), pages 439–448. IEEE, 2019.
[10] Ricky TQ Chen, Yulia Rubanova, Jesse Bettencourt, and David Duvenaud. Neural ordinary differential equations. arXiv preprint arXiv:1806.07366, 2018.
[11] Christopher Rackauckas, Mike Innes, Yingbo Ma, Jesse Bettencourt, Lyndon White, and Vaibhav Dixit. Diffeqflux.jl - A julia library for neural differential equations. CoRR, abs/1902.02376, 2019.
[12] Yang Song, Jascha Sohl-Dickstein, Diederik P Kingma, Abhishek Kumar, Stefano Ermon, and Ben Poole. Scorebased generative modeling through stochastic differential equations. arXiv preprint arXiv:2011.13456, 2020.
[13] Maziar Raissi, Paris Perdikaris, and George E Karniadakis. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378:686–707, 2019.
[14] Frank Noé, Alexandre Tkatchenko, Klaus-Robert Müller, and Cecilia Clementi. Machine learning for molecular simulation. Annual review of physical chemistry, 71:361–390, 2020.
[15] Maciej Majewski, Adrià Pérez, Philipp Thölke, Stefan Doerr, Nicholas E Charron, Toni Giorgino, Brooke E Husic, Cecilia Clementi, Frank Noé, and Gianni De Fabritiis. Machine learning coarse-grained potentials of protein thermodynamics. arXiv preprint arXiv:2212.07492, 2022.
[16] Mike Entwistle, Zeno Schätzle, Paolo A Erdman, Jan Hermann, and Frank Noé. Electronic excited states in deep variational monte carlo. arXiv preprint arXiv:2203.09472, 2022.
[17] J Quetzalcóatl Toledo-Marín, Geoffrey Fox, James P Sluka, and James A Glazier. Deep learning approaches to surrogates for solving the diffusion equation for mechanistic real-world simulations. Frontiers in Physiology, 12, 2021.
[18] Christoph Baur, Stefan Denner, Benedikt Wiestler, Nassir Navab, and Shadi Albarqouni. Autoencoders for unsupervised anomaly segmentation in brain mr images: A comparative study. Medical Image Analysis, page 101952, 2020.
[19] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 770–778, 2016.
[20] Kishan KC, Rui Li, and MohammadMahdi Gilany. Joint inference for neural network depth and dropout regularization. Advances in Neural Information Processing Systems, 34, 2021.
[21] Michael Innes, Elliot Saba, Keno Fischer, Dhairya Gandhi, Marco Concetto Rudilosso, Neethu Mariya Joy, Tejan Karmali, Avik Pal, and Viral Shah. Fashionable modelling with flux. CoRR, abs/1811.01457, 2018.
[22] Christopher Rackauckas and Qing Nie. Differentialequations.jl–a performant and feature-rich ecosystem for solving differential equations in julia. Journal of Open Research Software, 5(1), 2017.
[23] Andre˘ı Nikolaevich Tikhonov and Aleksandr Andreevich Samarskii. Equations of mathematical physics. Courier Corporation, 2013.
[24] J. Quetzalcoatl Toledo-Marin. Steady state diffusion surrogate. https://github.com/jquetzalcoatl/ DiffSolver, 2023.
[25] Diederik P Kingma and Jimmy Ba. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980, 2014.
[26] Peter J Huber. Robust estimation of a location parameter. In Breakthroughs in statistics, pages 492–518. Springer, 1992.
[27] Olaf Ronneberger, Philipp Fischer, and Thomas Brox. U-net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, October 5-9, 2015, Proceedings, Part III 18, pages 234–241. Springer, 2015.
[28] Ben Sorscher, Robert Geirhos, Shashank Shekhar, Surya Ganguli, and Ari S Morcos. Beyond neural scaling laws: beating power law scaling via data pruning. arXiv preprint arXiv:2206.14486, 2022.
[29] Jeyan Thiyagalingam, Mallikarjun Shankar, Geoffrey Fox, and Tony Hey. Scientific machine learning benchmarks. Nature Reviews Physics, 4(6):413–420, 2022.
This paper is available on arxiv under CC 4.0 license.