Authors:
(1) Nhat A. Nghiem, Department of Physics and Astronomy, State University of New York (email: nhatanh.nghiemvu@stonybrook.edu);
(2) Tzu-Chieh Wei, Department of Physics and Astronomy, State University of New York and C. N. Yang Institute for Theoretical Physics, State University of New York.
Table of Links
Acknowledgements, Declarations, Data Availability Statement, and References
II. APPLICATIONS
In this section, we highlight some interesting applications of the above simple procedure for matrix multiplication. We will soon appreciate a very remarkable efficiency that the above method yields.
A. Accelerating Eigenvalues Finding

where |Garbage⟩ is some unimportant state (not properly normalized). Combining such a procedure with the Hadamard test, the largest eigenvalue of A can be estimated. As mentioned in Theorem 1 of [5], the running time of the quantum power method is

where n is the dimension of A, s is the sparsity of A, κ is the conditional number of A, k is the number of iterations, and ϵ is the error tolerance (the additive approximation to the true largest eigenvalue).
While the speedup with respect to n is remarkable, we shall see that the improved matrix application 1 can improve the scaling on κ and ϵ. The crucial step in such a quantum power method is the HHL-like procedure, where the eigenvalues of A are extracted via quantum phase estimation, followed by rotation of ancilla controlled by the phase register. As can be seen from Theorem 1, matrix multiplication can be done very efficiently with the Chebyshev method [2]. The dependence on dimension n and conditional number κ and even tolerance error ϵ are all polylogarithmic. With such an improvement in performing matrix multiplication, we establish the following faster routine for quantum power method:
Theorem 2 Given coherent access to a Hermitian matrix A, its largest eigenvalue could be estimate to additive accuracy ϵ with running time
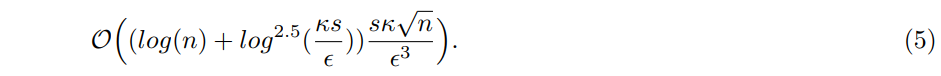
For simplicity purpose, if we neglect the contribution of logarithmic terms (compared to the polynomial terms), then we the faster QPW method has the same scaling on dimension n and sparsity s, almost quadratically better dependence on κ and a minor improvement on error ϵ.
B. Estimating Trace of a Matrix
We remark that the adaptive method in [4] has the same running time as the original HHL [1], which is quadratic in κ and polynomial in sparsity s. In our aforementioned result, the dependence on κ and s are polylogarithmic, which is thus highly efficient. It demonstrates the surprising utility of the Chebyshev series method introduced in [2]. As we have mentioned three examples above that rely on matrix multiplication, we foresee that matrix multiplication will be employed in other algorithms. The polylogarithmic dependence on all factors highlights that even if it is being used as a subroutine in a larger algorithm, the cost induced would be very modest. To exploit further the surprising efficiency of the above method, we now provide an alternative solution to the trace estimation problem of some given matrix. This problem has occured in [10], as estimating trace of kernel matrix is a necessary step of building (quantum) support vector machine. Additionally, this problem is also finds its application the DQC-1 model of quantum computation [11, 12], which can, e.g., efficiently estimate the values of Jones polynomials. We shall see that, in a similar fashion to the Chebyshev method [2], our method to estimate trace of a matrix would not make use of Hamiltonian subroutine, e.g., as in [10].

Then reverse the CNOT layers to return the old index. We obtain the following:
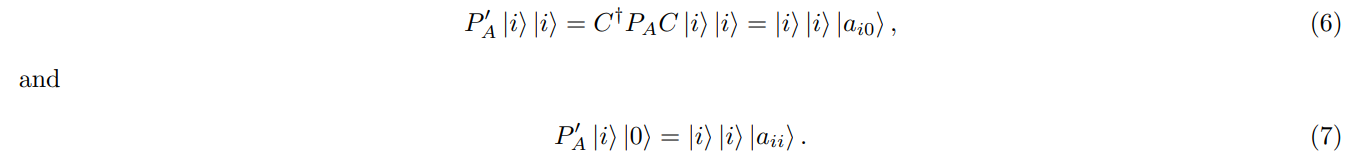
Effectively, the modified blackbox P ′ A would ‘return’ the new matrix that has entries in a different order compared to A. However, the first column of, say, A′ is exactly the diagonal entries of A. We remark that what we describe above is just a simple way to relocate the entries of given matrix A. Basically, one can opt to relocate, or permute entries of A in different ways, as long as the first column of the new matrix is the diagonal of A.
Now we are ready to describe our main algorithm. We note the following simple matrix multiplication identity:


• The first state is (see Lemma 1 for definition of U(A′ ) and m = log(2N) + 1)
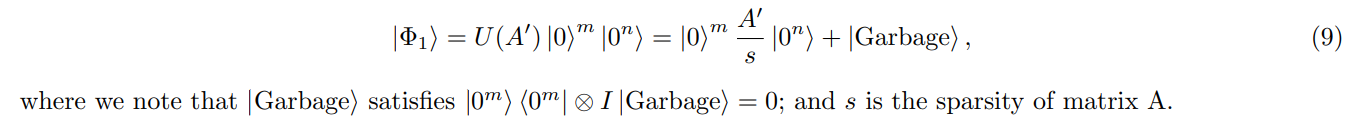
• The second state is

We have noted that this problem can be done easily using classical algorithm. We just simply need to query the matrix to get the diangonal entries and perform the summation, which can be done in logarithmic time using parallel algorithm. Therefore, classical computer can perform better in regards of time complexity. However, classical algorithm requires as much as N queries to matrix A in order to obtain diagonal entries. Meanwhile, in order to perform matrix multiplication, O(1) queries to matrix A is sufficient [2]. We remark that the above quantum running time is highly efficient w.r.t all parameters N, κ, s, as long as when κ and s grows polynomially as a function of N. For completeness, we restate the above quantum algorithm in the following theorem with the condition that the matrix A is not too ill-conditioned.
Theorem 3 Given coherent access to some Hermitian matrix A, then its trace can be estimated to additive accuracy δ in time
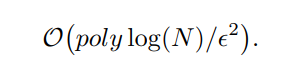
where the highest order of polylog(N) is about 2.

The inner product of the above two states is
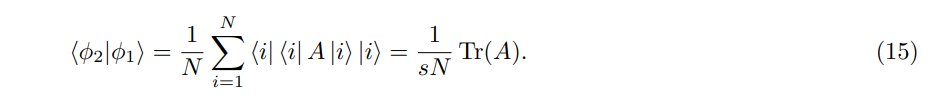
By using Hadamard test, we can estimate the real and complex part of Tr(A), or more precisely, of Tr(A)/(sN).
C. Estimating Trace of Product of Two Matrices
In the above method, we use the simple trick to relocate those diagonal entries of given matrix A. However, that trick is not convenient to use when dealing with the problem of estimating Tr(A · B) where A and B are two matrices of size N × N (we assume the same condition on the bound of their spectrum, as well as Hermitian property as in the previous section). Before diving into the quantum algorithm, we quickly review the computation of trace. Let C = A · B, then


Theorem 4 Given access to entries of two matrix A and B, the trace of AB could be estiamted to additive accuracy δ in time

In order to compute Tr(AB), matrix multiplication needs to be done before summing over the diagonal entries. There are many classical algorithms for matrix multiplication, but none are known for achieving such task within polylogarithmic time. Therefore, the quantum algorithm outlined above yields exponential speedup with respect to dimension N of given matrix.
D. Estimating Frobenius Norm
Given a Hermitian matrix A of size N × N, its Frobenius norm is computed as:

where {λi} are eigenvalues of A (note that since A is Hermitian then all eigenvalues are real). Revealing the full spectrum of A is apparently a daunting task. However, by definition, we have:

Hence, as straightforward as it seems, the square of Frobenius norm is a direct result of previous section, since we are able to apply the matrix A and A†. The running time is similar to equation (23).
As an alternative solution, now we describe how to compute such Frobenius norm with matrix application technique combined with quantum phase estimation. We first prepare the completely mixed state:

This paper is available on arxiv under CC 4.0 license.

